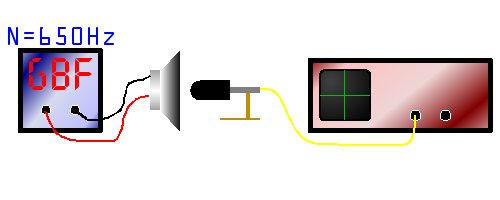
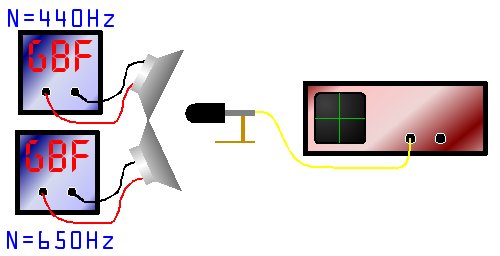
Pour pouvoir répondre à cette question, nous avons d'abord réalisé des expériences. Les résultats de ces expériences ont permis de déduire un théorème sur le mélange des sons purs, auquel vient s'ajouter le théorème plus général de Fourrier.
[ Expériences ]